Ejercicios de trigonometria

Hola!! hoy les traemos algunos ejercicios de trigonométrica, un tema que estuvimos viendo en algunas entradas anteriores, podran encontrar las respuestas al final:
                                                 TRIGONOMETRIA
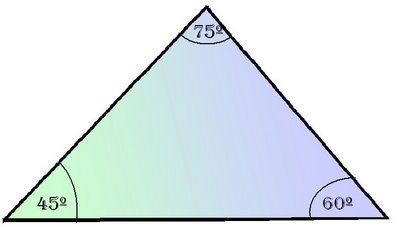
1)

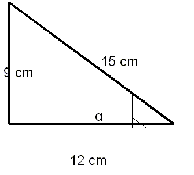
2)Calcula las razones trigonométricas del ángulo α :


3) Calcula la altura de la torre si nuestro personaje está a 7 m de la base de la
torre, el ángulo con el que está observando la cúspide es de 60º y sostiene el artilugio a una altura de 1,5 m.


Respuestas:
1)Este será el planteo a realizar:



2)Como ves, los tres lados del triángulo son conocidos, así que para calcular las razones trigonométricas sólo tenemos que aplicar las fórmulas y sustituir. Para el ángulo α el cateo opuesto es 9, el contiguo 12 y la hipotenusa 15.

                                  

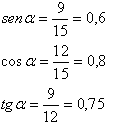
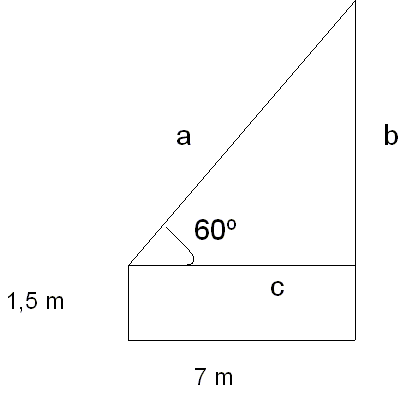3) 

Para comenzar, vamos a hacer un dibujo

que aclare un poco la situación poniendo los datos que conocemos.

Si nos fijamos en el triángulo, el lado c mide 7 m y una vez que tengamos calculado el lado b, para calcular la altura de la torre sólo tendremos que sumarle los 1,5 m. Así pues, vamos a calcular el lado b.

Para el ángulo 60º, el lado que conozco es el cateto contiguo y el que quiero calcular es el cateto opuesto, así pues planteo la tangente de 60º.



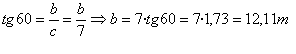
Por tanto la altura de la torre es 12,11 m + 1,5 m = 13, 61 m.

Lo resolvieron bien? esperamos que si, nosotros nos estaremos viendo la próxima semana, chau!

funciones trigonometricas

Hola!! hoy les vamos a presentar la segunda entrada de TRIGONOMETRIA.


                 Funciones  trigonometricas

Una función trigonométrica, también llamada circular, es aquella que se define por la aplicación de una razón trigonométrica a los distintos valores de la variable independiente, que ha de estar expresada en radianes.

SENO:

El seno del ángulo B es es la razón entre el cateto opuesto al ángulo y la hipotenusa.

Se denota por sen B.

El seno de un ángulo en una circunferencia goniométrica es igual a la ordenada.

COSENO:

El coseno del ángulo B es la razón entre el cateto contiguo al ángulo y la hipotenusa.

Se denota por cos B.

El coseno de un ángulo en una circunferencia goniométrica es igual a la abscisa.

TANGENTE:

La tangente del ángulo B es la razón entre el cateto opuesto al ángulo y el cateto contiguo al ángulo.

Se denota por tg B.

Tangente en la circunferencia goniométrica

Hasta aca con la entrada de hoy, espero que les haya servido y hasta la próxima semana!

¿Como ser un buen estudiante de matematicas?

Hola a todos, bienvenidos a otra nueva entrada. en el día de hoy les daremos unos tips para que puedan ser buenos estudiantes en matemáticas, ya que a veces no prestamos atención porque se torna un poco aburrido. Esperamos que les guste.

1

Asiste a las clases. Cuando faltas a una clase, tenes que aprenderte los conceptos con ayuda de un compañero o de tu libro. Nunca será igual el aprendizaje que obtengas de tus compañeros o de tu libro como el que te dará tu maestro.

• Llega a clase a tiempo. De hecho, llega un poco más temprano y abre tu cuaderno en el lugar correcto, abre tu libro y saca tu calculadora para que ya estés preparado para iniciar en cuanto tu maestro llegue.
• Solo falta a clase si estás enfermo. Si faltas, habla con un compañero para que te enteres de lo que enseñó el maestro y sepas lo que hay de tarea.

2

Resuelve junto con tu maestro. Si tu profesor resuelve problemas al frente de la clase, resuélvelo al mismo tiempo en tu cuaderno.

• Asegúrate de que tus notas sean claras y fáciles de leer. No solo escribas los problemas, también escribe cualquier cosa que el profesor diga que pueda ayudarte a entender mejor los conceptos.
• Resuelve todos los problemas de práctica que tu profesor te de. Cuando el maestro esté caminando por el salón mientras trabajas,consúltale tus dudas .
• Participa mientras el profesor resuelve el problema. No esperes a que el maestro te pregunte. Ofrécete para responder cuando conozcas la respuesta y levanta la mano para hacer preguntas cuando no estés seguro sobre algo que enseñe.

 3 Hace tu tarea el mismo día que se te asigne. Cuando haces la tarea el mismo día, los conceptos siguen frescos en tu mente. A veces no será posible terminar la tarea el mismo día, pero solo asegúrate de que tu tarea esté completa antes de que vayas a clase.

4

Esfuérzate fuera del salón si necesitas ayuda. Consulta a tu profesor durante su tiempo libre.

• Únete a un grupo de estudios. Los grupos de estudios contienen normalmente entre 4 y 5 personas con una buena mezcla de niveles de habilidad. Si eres de los que sacan 6 en matemáticas, entonces únete a un grupo que tenga 2 o 3 estudiantes que saquen 9 o 10 para que puedas aumentar tu nivel. Evita unirte a un grupo lleno de estudiantes cuyas notas sean menores a las tuyas.

Esperamos que esto les sirva de ayuda, para que les valla un poco mejor. Hasta la próxima!!!

Trigonometria

¡Hola! hoy vamos a empezar con una serie de entradas sobre la TRIGONOMETRÍA, hoy comenzaremos con lo mas básico de este tema.

TRIGONOMETRÍA

¿Qué es?

*La palabra trigonometría es un sustantivo, que deriva de dos raíces griegas: por una parte τριγωνο (trigōno = tres ángulos) o sea para nosotros “triángulo” y μετρον (metron) para nosotros “medida”.

*Trigonometría es literalmente el estudio de las relaciones existentes entre todas las medidas (de lados y ángulos) de un triángulo.

*Originalmente se utilizaba la trigonometría para definir las relaciones entre los elementos básicos de un triángulo, esto es los seis elementos principales: los 3 lados y 3 ángulos. No cualquiera tres segmentos pueden servir como los lados de un triángulo (han de cumplir una cierta relación para que el triángulo “cierre”). Por otra parte, no cualquieras tres ángulos pueden ser los ángulos de un triángulo: los tres ángulos de un triángulo suman un ángulo llano, es decir 180º.

Primero que todo debemos saber que los triángulos pueden clasificarse según sus lados y según sus ángulos. 

SEGÚN SUS LADOS:

TRIÁNGULO EQUILÁTERO

El triángulo equilátero es aquel que tiene todos sus lados de la misma medida.

TRIÁNGULO ISÓSCELES
El triángulo isósceles es aquel que tiene sólo dos lados de igual medida.

TRIÁNGULO ESCALENO

El triángulo escaleno es aquel que tiene todos sus lados de distinta medida.

SEGÚN SUS ÁNGULOS

TRIÁNGULO ACUTÁNGULO

El triángulo acutángulo es aquel que tiene todos sus ángulos agudos.

TRIÁNGULO RECTÁNGULO

El triángulo rectángulo es aquel que tiene un ángulo recto

TRIÁNGULO OBTUSÁNGULO

El triángulo obtusángulo es aquel que tiene un ángulo obtuso, tal como se muestra a continuación:

Resumiendo seria...

Esperamos que les haya gustado esta introducción a la trigonometría, en la próxima entrada hablaremos sobre las razones trigonométricas, hasta entonces!