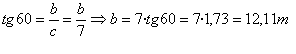Hola a todos, bienvenidos una vez más!El otro día mientras hacia mi tarea de matemática por alguna razón me pregunte; "¿cómo y cuándo se empezó a usar la matemática?... seguramente las personas ni siquiera se daban cuanta de que la estaban usando..." entonces empece a investigar un poco y la información que encontré me pareció bastante interesante como para compartirla con ustedes en el blog. Acá va:
El origen de la matemática
*La primera muestra de conceptos matemáticos en nuestros antepasados fue hallada en una cueva en Sudáfrica, y consiste en rocas de ocre adornadas con hendiduras con formas geométricas datadas en 70.000 años de antigüedad
*la primera evidencia arqueológica la encontramos en el hueso de Lebombo, hallado en Suazilandia y datado en 35.000 años de antigüedad. Este objeto es un peroné de babuino con un total de 29 hendiduras que, según las excavaciones arqueológicas que se llevaron a cabo en 1973, fueron usadas por las mujeres de la época para mantener la cuenta de sus ciclos menstruales, ya que otros huesos y piedras se han encontrado con entre 28 y 30 hendiduras, existiendo siempre una marca significativa en la última.

*El siguiente hito lo encontramos en el hueso de Ishango, hallado cerca del nacimiento del río Nilo, al noreste del Congo y con una antigüedad de entorno a 20.000 años. Este hueso contiene una serie de marcas a lo largo de él divididas en tres columnas. La asimetría de estas muescas hace pensar que estas fueron utilizadas con fines más funcionales que decorativase.

*Los textos matemáticos más antiguos disponibles son la tablilla de barro Plimpton 322 (c. 1900 a. C.), el papiro de Moscú (c. 1850 a. C.), el papiro de Rhind (c. 1650 a. C.) y los textos védicos Shulba Sutras (c. 800 a. C.).
*En todos estos textos se menciona el teorema de Pitágoras, que parece ser el más antiguo y extendido desarrollo matemático después de la aritmética básica y la geometría.
*Tradicionalmente se ha considerado que la matemática, como ciencia, surgió con el fin de hacer los cálculos en el comercio, para medir la Tierra y para predecir los acontecimientos astronómicos.
*Muchos textos griegos y árabes de matemáticas fueron traducidos al latín, lo que llevó a un posterior desarrollo de las matemáticas en la Edad Media.
*Desde tiempos ancestrales hasta la Edad Media, las ráfagas de creatividad matemática fueron seguidas, con frecuencia, por siglos de estancamiento. Pero desde el renacimiento italiano, en el siglo XVI, los nuevos desarrollos matemáticos, interactuando con descubrimientos científicos contemporáneos, fueron creciendo exponencialmente hasta el día de hoy.
Y hasta acá por el dia de hoy, esperamos que luego de leer este post se lleven un poco de conocimientos nuevos y que se hayan entretenido un poco, con esto me despido hasta la próxima semana :)

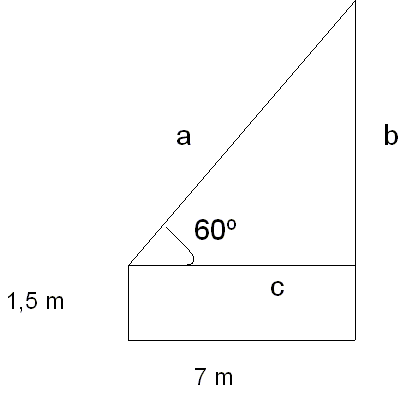
 3) Calcula la altura de la torre si nuestro personaje está a 7 m de la base de la
3) Calcula la altura de la torre si nuestro personaje está a 7 m de la base de la
 3)
3)